
En koordinattransformation är en konvertering av koordinater från ett koordinatsystem till ett annat. Beroende på tillämpning används olika transformationsmetoder.
Bakgrund
Koordinattransformationer görs till exempel för att kunna presentera olika datamängder tillsammans om de olika datamängderna inte redan redovisas i samma koordinatsystem.
Begreppet koordinattransformation kan användas allmänt för alla funktioner där man överför givna punktkoordinater i ett koordinatsystem (från-systemet) till en ny uppsättning koordinater i ett annat koordinatsystem (till-systemet).
Man brukar skilja mellan definitionsmässiga transformationssamband, som vi brukar kalla överräkningar, och empiriska samband, som vi brukar kalla inpassningsformler.
Definitionsmässiga transformationssamband
Definitionsmässiga transformationssamband används för transformation inom ett referenssystem.
I denna typ av transformationssamband är transformationsparametrarna fastslagna som konstanter, fast definierade. För att särskilja denna typ av transformation förekommer några olika, särskilda namn; koordinatomvandling och överräkning. På engelska används ofta termen "conversion" i detta sammanhang.
Exempel där definitionsmässiga transformationssamband används
- Omvandling av koordinatformat, till exempel från geocentriska SWEREF 99 till latitud, longitud och höjd över ellipsoiden i SWEREF 99:
(X,Y,Z) Û (j,l,h). - Kartprojektioner, till exempel från latitud och longitud i SWEREF 99 till SWEREF 99 TM:
(j,l) Û (N,E). - Byte av medelmeridian, till exempel från SWEREF 99 12 00 till SWEREF 99 TM:
(N,E) Û (j,l) Û (N,E).
Empiriska transformationssamband
Empiriska samband används för transformation mellan två referenssystem.
I empiriska transformationssamband tas transformationsparametrarna fram genom någon typ av inpassning, till exempel unitär transformation, Helmerttransformation eller direktprojektion (projektionsinpassning). Parametrarna bestäms alltså genom en inpassning av ett antal inmätta passpunkter.
Exempel där empiriska transformationssamband används
- Datumbyte, till exempel från geocentriska RT 90 till geocentriska SWEREF 99:
(X,Y,Z) Û (X,Y,Z). - Plan transformation, till exempel från RT 90 5 gon V 0:-15 till lokalt system:
(x,y) Û (x,y). - Direktprojektion, till exempel från latitud och longitud i SWEREF 99 till lokalt system (RIX 95-sambanden är oftast av denna typ):
(j,l) Û (x,y).
Inpassning
Inpassning betyder att man bestämmer de numeriska värdena på parametrarna i en transformationsformel, baserat på att ett antal punkter, passpunkterna, som har kända koordinater i både till- och från-systemen. Olika transformationsmetoder kräver olika antal passpunkter för att ge en entydig bestämning av parametrarna.
| Transformationsmetod | Antal passpunkter |
|---|---|
| Translation | 1 |
| Unitär | 2 |
| Helmert, tvådimensionell | 2 |
| Affin | 3 |
Eftersom passpunkternas koordinater, som används vid inpassningen, har tillkommit genom något mätförfarande är de inte felfria. För att minimera den inverkan som felen i koordinaterna har på beräkningen av parametrarna använder man normalt fler än det antalet gemensamma punkter som krävs. Önskvärt är också att punkterna är väl spridda över det område man ska transformera.
När fler punkter än de som krävs används, beräknas parametrarna med hjälp av minsta kvadrat-metoden. Genom denna metod minimerar man motsättningarna mellan passpunkternas koordinater i till-systemet och motsvarande koordinater som fås genom transformation av koordinaterna i från-systemet. Tillvägagångssättet ger även en möjlighet att skatta hur mycket transformationen bidrar till felet i de transformerade koordinaterna.
Olika transformationsmetoder i två dimensioner
Translation
Translation är en empirisk transformationsmetod som endast består av förflyttning av origo med två konstanter, en i x-led och en i y-led.
Parametrarna x0 och y0 kan bestämmas genom ett inpassningsförfarande.
I specialfallet då translation används för att kompensera för ett lokalt origo är dock parametrarna definitionsmässiga.
Formelsamband
Formelsambandet för transformationsmetoden translation är:
xt = x0 + xf
yt = y0 + yf
där (xf, yf) är koordinaterna i från-systemet och (xt, yt) är koordinaterna i till-systemet.
Unitär transformation
Unitär transformation är en typ av likformighetstransformation med tre parametrar. Det är en empirisk transformationsmetod, där parametrarna bestäms genom ett inpassningsförfarande.
Parametrarna är:
- Två translationer, x0 och y0
- En vridning, α
Transformationsmetoden används i de fall skalan ska vara oförändrad mellan från- och till-systemen. Oförändrad skala är i vissa fall ett villkor då uppmätta längder och arealer skall vara oförändrade.
Formelsamband
Formelsambandet för unitär transformation är:
xt = x0 + xf · cos α - yf · sin α
yt = y0 + xf · sin α + yf · cos α
där (xf, yf) är koordinaterna i från-systemet och (xt, yt) är koordinaterna i till-systemet.
Helmerttransformation
Helmerttransformation definieras av fyra parametrar och är den vanligaste plana transformationsmetoden inom geodesin.
Metoden tar hänsyn till att systemen inte har sammanfallande origon, att koordinataxlarna inte är parallella och att systemen inte har samma skala. Parametrarna är alltså:
- Två translationer, x0 och y0
- En vridning, α
- En skalfaktor, m
Detta innebär att formen på objekt inte förändras vid en Helmerttransformation. Metoden är en empirisk transformationsmetod och parametrarna bestäms därmed genom ett inpassningsförfarande.
Figuren ger dig en uppfattning om hur sambandet i princip kan se ut.
Formelsamband
Beteckna koordinaterna i det system som vi transformerar från med (xf, yf) och koordinaterna i det system vi transformerar till med (xt, yt). Enligt figuren gäller då för en godtycklig punkt P följande samband:
xt = x0 + xf · m · cos α - yf · m · sin α
yt = y0 + xf · m · sin α + yf · m · cos α
där (xf, yf) är koordinaterna i från-systemet och (xt, yt) är koordinaterna i till-systemet.
Formlerna ovan tar hänsyn till skiftet i origo (x0, y0) och koordinataxlarnas bristande parallellitet, vridningen α. För att kompensera för skillnaden i skala multipliceras koordinaterna i från-systemet med skalfaktorn m.
Ekvationerna snyggas till genom att sätta
a = m · cos α
b = m · sin α
och vi får
xt = x0 + a · xf - b · yf
yt = y0 + b · xf + a · yf
Man brukar kalla storheterna x0 , y0 , a och b för Helmertsambandets parametrar. Som nämndes inledningsvis bestäms de numeriska värdena på parametrarna genom inpassning.
Affin transformation
Affin transformation kan användas när det finns risk att skalorna i x- och y-led är olika, till exempel vid digitalisering från papperskartor som har ändrat form.
Affin transformation är en deformerande transformationsmetod. Metoden är en empirisk transformationsmetod och parametrarna bestäms därmed genom ett inpassningsförfarande. De parametrar som ingår i metoden är:
- Två translationer, x0 och y0
- En vridning, a
- Två skalfaktorer, mx och my
- Bristande rätvinklighet, affinitet, b
Formelsamband
Beteckna koordinaterna i det system som vi transformerar från med (xf , yf) och koordinaterna i det system vi transformerar till med (xt , yt). Sambandet kan då sättas upp som:
xt = x0 + xf · mx · cos α - yf · my · sin(α + β)
yt = y0 + xf · mx · sin α + yf · my · cos(α + β)
där (xf, yf) är koordinaterna i från-systemet och (xt, yt) är koordinaterna i till-systemet.
Formlerna ovan tar hänsyn till skiftet i origo (x0, y0), koordinataxlarnas bristande parallellitet, vridningen a, den bristande rätvinkligheten, b, och för att kompensera för skillnaden i skala multipliceras koordinaterna i från-systemet med skalfaktorerna mx och my.
Ekvationerna snyggas till genom att sätta
a = mx · cos α
b = -my · sin(α + β)
c = mx · sin α
d = my · cos(α + β)
och vi får
xt = x0 + a · xf + b · yf
yt = y0 + c · xf + d · yf
Man brukar kalla storheterna x0 , y0 , a, b, c och d för den affina transformationens parametrar. Som nämndes inledningsvis bestäms de numeriska värdena på parametrarna genom inpassning.
Olika transformationsmetoder i tre dimensioner
Helmerttransformation
Tredimensionell Helmerttransformation definieras av sju parametrar och kallas därför också 7-parametertransformation.
Denna typ av transformation används i samband med kartesiska tredimensionella system, som vanligen är inplacerade geocentriskt (eller nära geocentriskt), det vill säga att origo sammanfaller med jordens fysiska tyngdpunkt.
Tredimensionella inpassningsformler beräknas ur empiriska data på motsvarande sätt som vid plana inpassningar, men med tre koordinater (X, Y, Z) givna för varje passpunkt i från- och till-systemen.
Tredimensionell likformighetstransformation
(7-parameter, Bursa-Wolf)
En likformighetstransformation definieras av:
- Tre translationer: DX, DY, DZ
- Tre rotationer – en runt varje koordinataxel: wX, wY, wZ
- En skalförändring, som vanligen uttrycks som en skalkorrektion i ppm: d
I matrisform blir uppställningen:
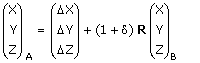
Där R är rotationsmatrisen enligt:
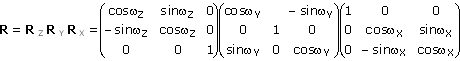
Den strikta inversen till samma formel ställs upp enligt:
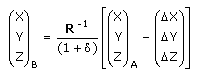
Där R-1 är den inversa matrisen till R. För rotationsmatriser gäller att R-1 = RT, det vill säga att inversen är lika med transponatet till den fullständiga rotationsmatrisen R. (Transponatet av en matris erhålls genom att kasta om rader och kolumner i matrisen.)
Observera att 7-parameterformeln kan ställas upp på lite olika sätt, när det gäller ordningen på operationerna och hur tecken på vridningar och skalfaktor ska tolkas. Därför bör du vid inläggning av parametrar i ett program alltid försäkra dig om att programmet tillämpar samma konventioner som det program som använts för skattningen av parametrarna.
Som ett minimum bör du verifiera inläggningen med hjälp av en kontrollpunkt med kända från- respektive transformerade koordinater.
X,Y,Z till latitud, longitud, ellipsoidhöjd
Omvandlingen mellan geocentriska och geodetiska koordinater sker med ett definitionsmässigt transformationssamband.
Det förekommer flera olika angreppssätt för att transformera mellan geocentriska koordinater (X,Y,Z) och geodetiska koordinater (latitud, longitud och höjd över ellipsoiden).
I formelbeskrivningen nedan används en sluten approximativ formel, men iterativa förfaranden är också vanliga. Skillnaden mellan den slutna formeln och ett iterativt förfarande kan maximalt uppgå till någon tiondels millimeter för normala tillämpningar i Sverige (höjden < 20 000 m).
De formler som används för att konvertera mellan de olika koordinattyperna finns, tillsammans med ett numeriskt exempel, i dokumentet Transformation mellan geocentriska kartesiska koordinater och geodetiska koordinater (pdf, nytt fönster).

